TMM4100 Materialteknikk

Hjem Atomstruktur Krystallstruktur Polymerstruktur Imperfeksjoner Diffusjon Mekaniske egenskaper Styrkemekanismer Svikt Fasetransformasjon Metaller Keramer Polymerer Kompositter Termiske egenskaper Elektriske egenskaper Korrosjon Materialvalg Diverse tema Case-studier

Introduksjon Temperaturavhengighet Stasjonær diffusjon Transient diffusjon

Transient diffusjon

Når diffusjonskoeffisienten er uavhengig av konsentrasjon, er Fick's 2. lov for 1-dimensjonelt tilfelle gitt ved

\begin{equation} \frac{\partial C}{\partial t}= D \frac{\partial^2 C}{\partial x^2} \tag{1} \end{equation}

I praksis kan (1) bare løses analyttisk for enkle grensebetingelser og initialbetingelser. Eksemplene i denne introduksjonen er løst numerisk med Eulers metode.

MERK: Forståelse av Eulers metode er ikke pensum i TMM4100, men du skal være i stand til å beskrive ulike transiente diffusjonsforløp som eksemplene illustrerer. Eksemplene blir gjennomgått i forelesning.

Eksempel-1:

Eksempel-2:

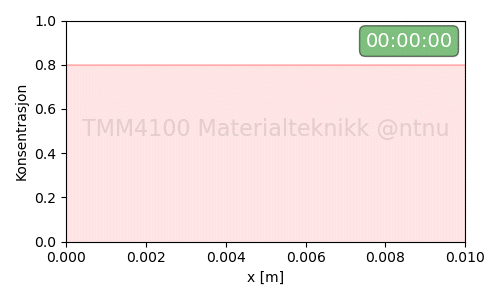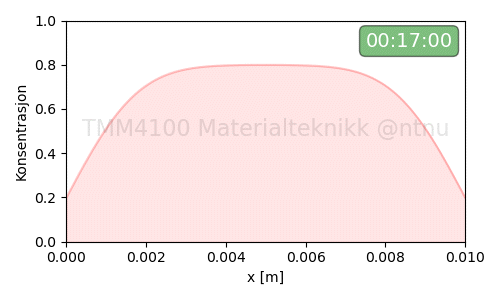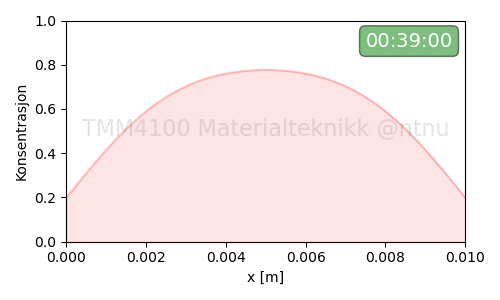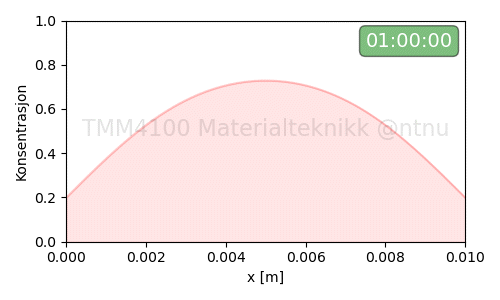
Eksempel-3:

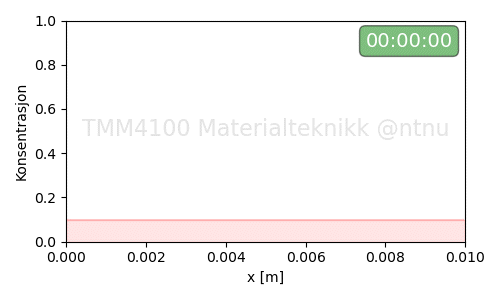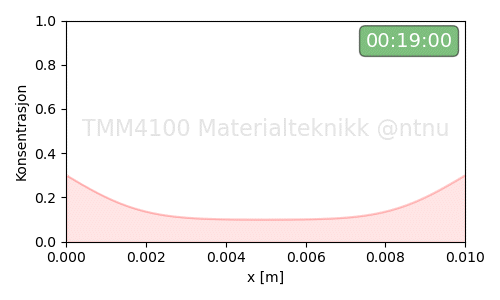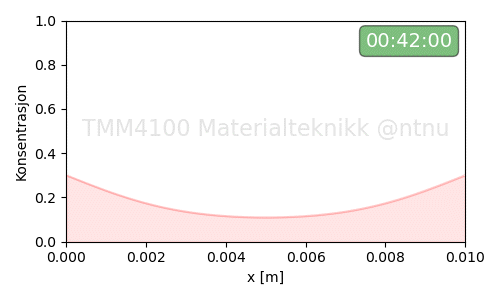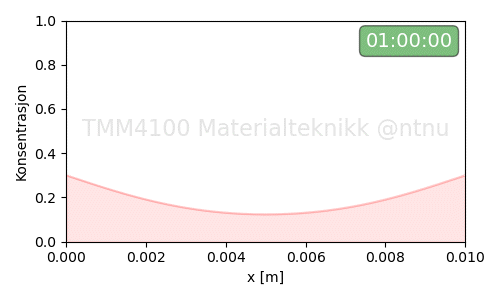
Eksempel-4:

Analytisk løsning for semi-uendelig plate

Analytiske løsninger for spesifikke tilfeller (gitte grensebetingelser osv.) er nokså begrenset. I TMM4100 er kun analytisk løsning for semi-uendelig plate inkludert i pensum:

\begin{equation} \frac{C_x - C_0}{C_s - C_0}=1-\text{erf}\Big(\frac{x}{2\sqrt{Dt}}\Big) \tag{2} \end{equation}

$C_x$: Konsentrasjon som funksjon av $x$

$C_0$: Initiell uniform konsentrasjon

$C_s$: Konsentrasjon ved $x$=0

$D$: Diffusjonskoeffisient

$t$: Tid

Erf-funksjonen

Siden løsningen involverer erf-funksjonen, kan det være lurt (særlig på eksamen...) å ha en intuitiv forståelse av denne, så her er den:

import numpy as np
import matplotlib.pyplot as plt
from scipy import special
%matplotlib inline

def plotErrorFunksjonen():
    z=np.linspace(0,2.5,251)
    erfz=special.erf(z)
    fig,ax=plt.subplots(figsize=(6,4))
    ax.plot(z,erfz)
    ax.grid(True)
    plt.xticks(np.arange(0,2.51,0.5))
    plt.yticks(np.arange(0,1.01,0.1))
    
    ax.set_xlim((0,2.5))
    ax.set_ylim((0,1))
    ax.set_xlabel('z')
    ax.set_ylabel('erf(z)')
    gridlines = ax.get_xgridlines() + ax.get_ygridlines()
    for line in gridlines:
        line.set_linestyle('-.')

plotErrorFunksjonen()

Nyttig observasjon: For $z > 2$ er funksjonsverdien tilnærmet 1 for de fleste praktiske problem.

Eksempel-1

D  = 1E-9    # diffusjonskoeffisient
X  = 0.01    # tykkelse (eller egentlig betraktet lengde)
nx = 50      # antall segment
Cs = 0.10    # konsentrasjon ved x=0
C0 = 0.00    # initiell konsentrasjon
t  = 1000    # tid for beregningen

x = np.linspace(0, X, nx+1)   
er= special.erf(x/(2*(D*t)**0.5))
Cx=(1-er)*(Cs-C0)+C0

#Plot

fig,ax=plt.subplots(figsize=(8,5))
ax.plot(x,Cx,color='green')
ax.set_title('Konsentrasjon ved t = '+str(t)+' s')
ax.set_xlabel('x')
ax.set_ylabel('Konsentrasjon')
ax.set_xlim(0,X)
ax.set_ylim(0,)
ax.grid(True)
plt.tight_layout()
plt.show()

Eksempel-2

D  = 1E-9    # diffusjonskoeffisient
X  = 0.01    # tykkelse (eller egentlig betraktet lengde)
nx = 100      # antall segment
Cs = 0.10    # konsentrasjon ved x=0
C0 = 0.00    # initiell konsentrasjon
ts  = (1E2,1E3,1E4,1E5)    # tider for beregning

fig,ax=plt.subplots(figsize=(8,5))
for t in ts: 
    x = np.linspace(0, X, nx+1)   
    er= special.erf(x/(2*(D*t)**0.5))
    Cx=(1-er)*(Cs-C0)+C0
    ax.plot(x,Cx,label='t ='+str(t)+' s')

ax.set_title('Konsentrasjonsprofil ved ulike tider')
ax.set_xlabel('x')
ax.set_ylabel('Konsentrasjon')
ax.set_xlim(0,X)
ax.set_ylim(0,)
ax.grid(True)
ax.legend(loc='best')
plt.tight_layout()
plt.show()

Eksempel-3

D    = 1E-9    # diffusjonskoeffisient
Cs   = 0.10    # konsentrasjon ved x=0
C0   = 0.00    # initiell konsentrasjon
x    = 0.005   # posisjon for utregningen
tmax = 1E5


t = np.linspace(1, tmax,200)   
er= special.erf(x/(2*(D*t)**0.5))
Cx=(1-er)*(Cs-C0)+C0

#Plot

fig,ax=plt.subplots(figsize=(8,5))
ax.plot(t,Cx,'--', color='green')
ax.set_title('Konsentrasjon ved x = 0.005 som funksjon av tid')
ax.set_xlabel('t')
ax.set_ylabel('Konsentrasjon')
ax.set_xlim(0,1E5)
ax.set_ylim(0,)
ax.grid(True)
plt.tight_layout()
plt.show()

Disclaimer:This site is designed for educational purposes only. There are most likely errors, mistakes, typos, and poorly crafted statements that are not detected yet... www.ntnu.edu/employees/nils.p.vedvik

Copyright 2023, All rights reserved