Shell elements and laminate theory¶
Overview¶
From abaqus documentation, with translation to laminate theory variables as used in this course:
SF1: Direct membrane force per unit width in local 1-direction. ( $N_x$ )
SF2: Direct membrane force per unit width in local 2-direction. ( $N_y$ )
SF3: Shear membrane force per unit width in local 1–2 plane. ( $N_{xy}$ )
SF4: Transverse shear force per unit width in local 1-direction.
SF5: Transverse shear force per unit width in local 2-direction.
SF6: Thickness stress integrated over the element thickness.
SM1: Bending moment force per unit width about local 2-axis. ( $M_x$ )
SM2: Bending moment force per unit width about local 1-axis. ( $M_y$ )
SM3: Twisting moment force per unit width in local 1–2 plane. ( $M_{xy}$ )
SE1: Direct membrane strain in local 1-direction. ( $\varepsilon_x^0$ )
SE2: Direct membrane strain in local 2-direction. ( $\varepsilon_y^0$ )
SE3: Shear membrane strain in local 1–2 plane. ( $\gamma_{xy}^0$ )
SE4: Transverse shear strain in the local 1-direction.
SE5: Transverse shear strain in the local 2-direction.
SE6: Total strain in the thickness direction.
SK1: Curvature change about local 2-axis. ( $\kappa_x$ )
SK2: Curvature change about local 1-axis. ( $\kappa_y$ )
SK3: Surface twist in local 1–2 plane. ( $\kappa_{xy}$ )
Demonstrations¶
A script for a shell based layered plate is presented in Abaqus Scripting, Shell laminate and can be used to replicate the examples here.
Figure-1 shows a shell based FEA model of a laminate subjected to a prescribed tensile strain in the $x$-direction imposed as displacements on the edges.
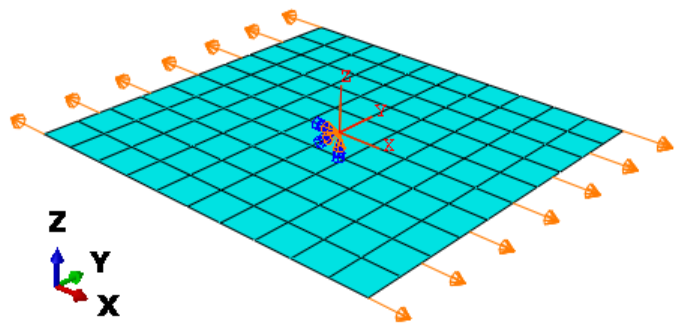
Figure-1: Laminate model
Dimensions: 100 x 100 x $h$, where the thickness $h$ is given by the section properties (layup)
Mesh: 10 x 10 elements of type S4R
Boundary conditions:
- The node at origo is fixed for all DOF (both translations and rotations)
- On the edge at $x$ = 50: $u_x$ = 0.5
- On the edge at $x$ = -50: $u_x$ = -0.5
The boundary conditions for the node at origo will maintain the conditions: $w = 0$ and $\frac{\partial w}{\partial x}$ for $(x,y)$ = (0,0), see Laminate deformation.
The laminate midplane strain $\varepsilon_x^0$ becomes:
\begin{equation} \varepsilon_x^0 = \frac{\Delta u_x}{\Delta x} = \frac{0.5 -(-0.5)}{100}=0.01 \end{equation}Example-1:¶
Consider a [0/90] laminate with the material, layup and loading as follows:
from laminatelib import laminateStiffnessMatrix, solveLaminateLoadCase, laminateThickness, layerResults
import numpy as np
m1={'E1':140000, 'E2':8000, 'v12':0.27, 'G12':5000,
'XT':1000, 'YT':50, 'XC':800, 'YC':200, 'S12':50, 'S23':50, 'f12':-0.5}
layup1 =[ {'mat':m1 , 'ori': 0 , 'thi':1} ,
{'mat':m1 , 'ori': 90 , 'thi':1} ]
LSM1 = laminateStiffnessMatrix(layup1)
result = solveLaminateLoadCase(LSM1,ex=0.01)
N=result[0]
D=result[1]
print('Loads=',np.round(N,1))
print('Deformations=',np.round(D,6))
Abaqus provides results for laminate loads and deformations as Section forces and moments and Section strains and curvatures. These must be specified in the Field Output Request for the step. The FEA results are:

Figure-2: FEA-results: Laminate loads and deformations
The field output variables translate to:
- SF1 = $N_x$
- SE1 = $\varepsilon_x^0$
- SE2 = $\varepsilon_y^0$
- SK1 = $\kappa_x$
Out-of-plane displacement $u_z$ (=$w$) is:
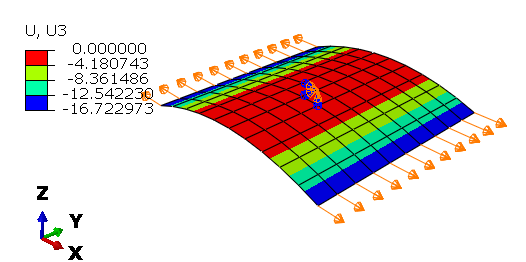
Figure-3: FEA-results: out-of-plane displacement
We can now compare the FEA results to the analytical displacement field derived in Laminate deformation:
\begin{equation} w(x,y) = -\frac{1}{2}\kappa_x x^2 -\frac{1}{2}\kappa_y y^2 -\frac{1}{2} \kappa_{xy} x y \end{equation}For example, at $(x,y)$ = (50,50):
print( 'w=' , (- D[3]*50**2 - D[4]*50**2 - D[5]*50*50)/2 )
def illustrateCurvatures(Kx,Ky,Kxy):
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import numpy as np
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax = fig.gca()
X = np.arange(-0.5, 0.6, 0.1)
Y = np.arange(-0.5, 0.6, 0.1)
X, Y = np.meshgrid(X, Y)
Z1 = (- Kx*X**2 - Ky*Y**2 - Kxy*X*Y)/2
surf1 = ax.plot_surface(X, Y, Z1, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
illustrateCurvatures(D[3],D[4],D[5])
The stresses in the material coordinate system at the top of the last layer (layer-2) is:
layres=layerResults(layup=layup1,deformations=D)
print( layres[-1]['stress']['123']['top'] )
The corresponding FEA results are:
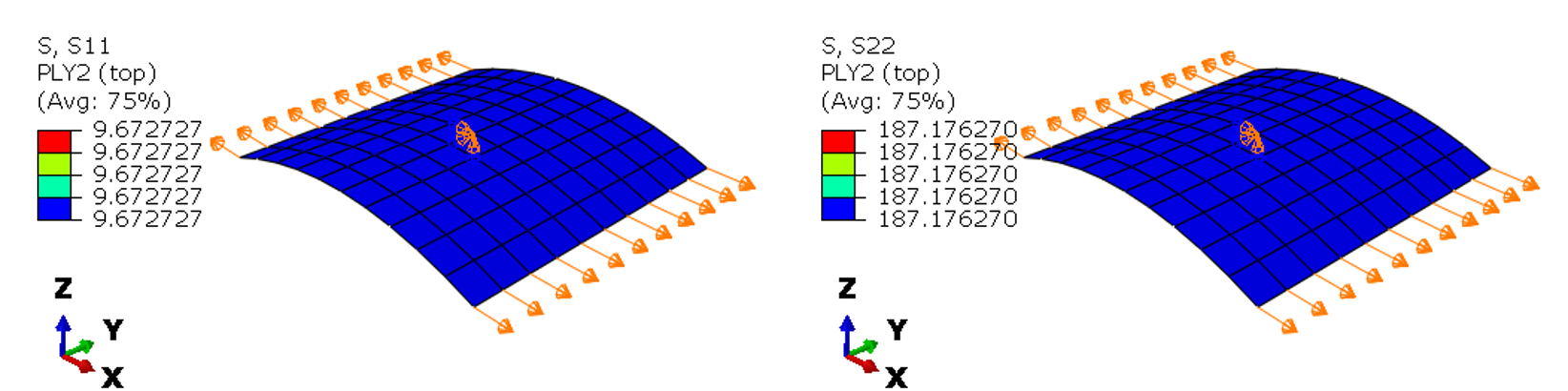
Figure-4: FEA-results: stresses
Example-2:¶
Consider a [-45/45] laminate with the material, layup and loading as follows:
m1={'E1':140000, 'E2':8000, 'v12':0.27, 'G12':5000,
'XT':1000, 'YT':50, 'XC':800, 'YC':200, 'S12':50, 'S23':50, 'f12':-0.5}
layup1 =[ {'mat':m1 , 'ori': -45 , 'thi':1} ,
{'mat':m1 , 'ori': 45 , 'thi':1} ]
LSM1 = laminateStiffnessMatrix(layup1)
result = solveLaminateLoadCase(LSM1,ex=0.01)
N=result[0]
D=result[1]
print('Loads=',np.round(N,1))
print('Deformations=',np.round(D,6))
Abaqus:

Figure-5: FEA-results: SK3 = $\kappa_{xy}$ and out-of-plane displacement
The out-of-plane displacement at the corner +$x$ and +$y$ is:
print( 'w=' , (- D[3]*50**2 - D[4]*50**2 - D[5]*50*50)/2 )
illustrateCurvatures(D[3],D[4],D[5])


