Laminates¶
A laminate is an assembly of joined layers where individual layers may consist of different materials and have different orientations and thicknesses.
Composite structures are often found as laminated plates and shells and many high performance light-weight structures are made of composite laminates. The reasons are many and are introduced successively during this part. One notable reason can be articulated by the simple argument: Unidirectional fiber composites enables outstanding specific properties in the fiber direction, and a laminated structure made of these materials enables different fiber orientations and tailor-made design for the specific application.
Definitions and notation¶
A laminate is a layered structure of laminae (singular: lamina) or layers. The term layer is commonly used in mechanical and mathematical description of laminates, while the term ply is used for a sheet of material that is applied to a laminate. Although the terms layers and plies are frequently used interchangeably, it is often important to make a consistent destinction between the two as illustrated in Figure-1: In the region to the left, there are 3 layers (Layer 1, Layer 2 and Layer 3) consisting of Ply 1, Ply 3 and Ply 4.

Figure-1: Example of plies versus layers
The layer orientation is defined as the angle of rotation $\theta$ about the $z$-axis of the laminate coordinate system ($x,y,z$). A layer coordinate system is generally alligned with the material coordinate system for that specific layer material, and identified by the axis 1,2,3.
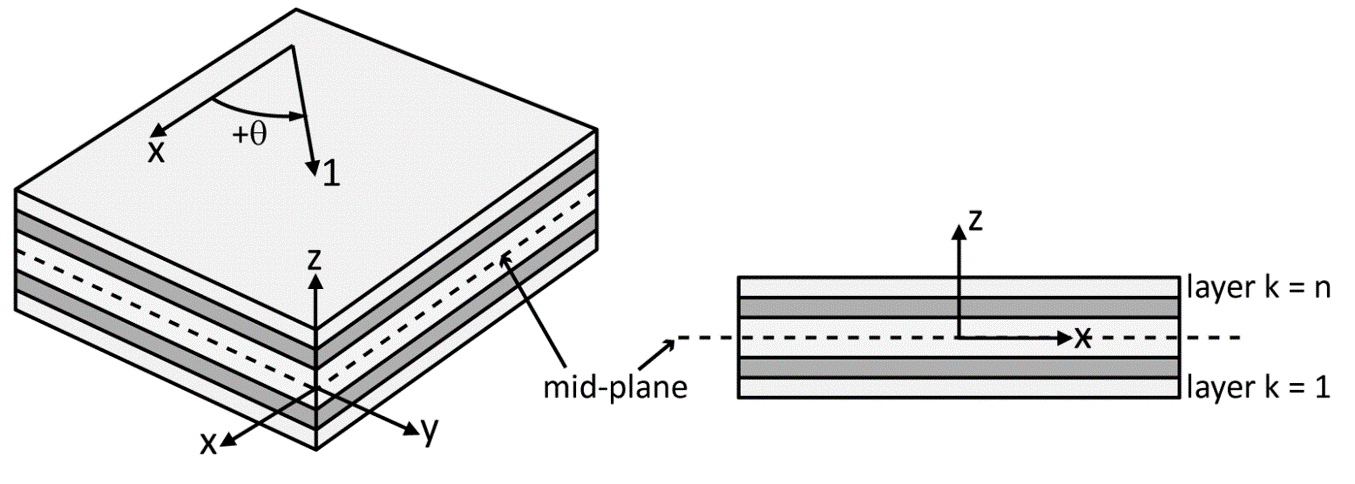
Figure-2: Laminate definitions
A layup can be described in various ways. For laminates consisting of only one material and where all layers have the same thicknesses, the sequence of orientation angles is sufficient. The layup starts from the bottom such that
[0 / 90 / -45 / 45]
implies that the bottom layer ($k=0$) has 0-degree orientation and the top layer ($k=4$) has a 45-degree orientation.
A symmetric laminate can indicated by a subscript s:
[0 / 90 / -45 / 45]s = [0 / 90 / -45 / 45 / 45 / -45 / 90 /0]
and a layup with a repating sequence indicated by a subscript number as in the following example:
[0/ 90/ -45 / 45]n = [0 / 90 / -45 / 45 / 0 / 90 / -45 / 45 / 0 / 90 / -45 / 45] for n = 3
Sometimes it can be convenient to write a repating subset of layers as the following example:
[(0 / 90)3 /-45/45] = [0 / 90 / 0 / 90 / 0 / 90 / -45 / 45]
A symmetric laminate has perfect symmetry about the mid-plane. Some examples:
[ 0 / 90 / 0], [-45 / 45 / -45] and [0 / 90 / -45 / 45 / 45 / -45 / 90 /0]
A balanced laminate is such that for every layer with orientation $\theta$, there exists another layer with the same material and same thickness and with an orientation -$\theta$. Examples:
[-45 / 45 / -45 / 45], [0 / 90 / 0].
Note that -90 orientation is identical to 90 orientation from a mechanical point of view.
Defining a lay-up¶
A layup is simply a sequence of layers where information about individual layers must include material properties, thickness and orientation angle. Hence, a layup is a table-like structure, and a list of dictionaries is one obvious choice when using Python. The length of the list is equal to the number of layers while each layer is defined by a dictionary having material (mat), orientation (ori) and thickness (thi):
m1={'name':'UDGRP', 'units':'MPa-mm-Mg','rho':2000E-9,
'E1':40000, 'E2':10000, 'v12':0.3, 'G12':3000}
layup1 = [ {'mat':m1 , 'ori': 0 , 'thi':0.5} ,
{'mat':m1 , 'ori': 90 , 'thi':0.5} ,
{'mat':m1 , 'ori': 45 , 'thi':0.25} ,
{'mat':m1 , 'ori':-45 , 'thi':0.25} ]
Python tips & tricks¶
The function illustrateLayup(layup,size) found in Plot Library creates an illustration of the layup:
from plotlib import illustrateLayup
%matplotlib inline
illustrateLayup(layup1,size=(4 , 1.2))
Since many layups are symmetric (reasons for that to be discussed later), it is useful to have a function that generates a complete symmetric laminat from half of the layers:
from copy import deepcopy
def symmetricLayup(layup):
for layer in reversed(layup):
layup.append(deepcopy(layer))
Note: the function deepcopy is required for making an independent copy of a dictionary (a layer in this case) instead of just a pointer to the same object.
symmetricLayup(layup1)
illustrateLayup(layup1,size=(4,2.5))
Many laminates have repeating sequences of a few basic layers. A useful function for those cases:
def repeatLayers(layup,count):
n=len(layup)
for c in range(0,count):
for k in range(0,n):
layup.append(deepcopy(layup[k]))
layup2 = [ {'mat':m1 , 'ori': 0 , 'thi':0.5} ,
{'mat':m1 , 'ori': 90 , 'thi':0.5} ]
repeatLayers(layup2,4)
illustrateLayup(layup2,size=(4,4))
Automatically construct a string for the simplified description (orientations only):
def simplifiedLayupDescription(layup):
orientations='/'
for layer in layup:
orientations=orientations+str(layer['ori'])+' / '
return orientations
print( simplifiedLayupDescription(layup1))
Compute the total thickness:
sum( [layer['thi'] for layer in layup1] )
Compute the mass per unit area of a laminate:
def laminateMass(layup):
return sum( [layer['mat']['rho']*layer['thi'] for layer in layup])
laminateMass(layup1)
(6E-6 Mg/mm2 which is equal to 6 kg/m2, you may add some logic that takes the units into consideration in the code)


