Hooke's Law¶
Hooke's law represents the linear relations between stresses and strains.
Tensor notation¶
Using the tensor notation, or index notation, we can state the general Hooke's law as
\begin{equation} \varepsilon_{ij} = S_{ijkl}\sigma_{kl} \tag{1} \end{equation}From the Einstein summation convention this is equivalent to \begin{equation} \varepsilon_{ij} = \sum_{k=1}^{3}\sum_{l=1}^{3}S_{ijkl}\sigma_{kl} \tag{2} \end{equation}
where $S_{ijkl}$ is called the compliance tensor. The stiffness tensor $C_{ijkl}$ is found in the inverse relation,
\begin{equation} \sigma_{ij} = C_{ijkl}\varepsilon_{kl} \tag{3} \end{equation}Both the stiffness tensor and the compliance tensor are fourth-order tensors that can be represented by arrays of dimensions (3 x 3 x 3 x 3)
Note that for one component of strain, there are 9 terms in the summation:
\begin{equation} \varepsilon_{ij} = \sum_{k=1}^{3}\sum_{l=1}^{3}S_{ijkl}\sigma_{kl} = S_{ij11}\sigma_{11}+S_{ij12}\sigma_{12}+S_{ij13}\sigma_{13}+S_{ij21}\sigma_{21}+S_{ij22}\sigma_{22}+S_{ij23}\sigma_{23}+S_{ij31}\sigma_{31}S_{ij32}\sigma_{32}+S_{ij33}\sigma_{33} \tag{4} \end{equation}Hence, there are 9 x 9 = 81 numerical values in both the compliance and in the stiffness tensor.
Most of the values are however zero or redundant due to the inherent symmetry required for satisfying the physics of the relation. Implementation of Hooke's law using this notation is straigth forward but not efficient since the data structure for both stresses, strains and compliance or stiffness must allocate recources that do not contribute to anything.
Matrix notation¶
Recall from the sections about stress and strain that both the stress tensor and the strain tensor is symmetric. Therfore, there are only 6 independent components of stress and 6 independet components of strain, and we may express the tensors in a vector form. The relation between the stress and the strain will now be a 6 x 6 matrix. For a general anisotropic material we will express Hooke's law by engineering components of stress and strain as:
\begin{equation} \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \gamma_{23} \\ \gamma_{13} \\ \gamma_{12} \end{bmatrix} = \begin{bmatrix} S_{11} & S_{12} & S_{13} & S_{14} & S_{15} & S_{16} \\ S_{12} & S_{22} & S_{23} & S_{24} & S_{25} & S_{26} \\ S_{13} & S_{23} & S_{33} & S_{34} & S_{35} & S_{36} \\ S_{14} & S_{24} & S_{34} & S_{44} & S_{45} & S_{46} \\ S_{15} & S_{25} & S_{35} & S_{45} & S_{55} & S_{56} \\ S_{16} & S_{26} & S_{36} & S_{45} & S_{56} & S_{66} \end{bmatrix} \begin{bmatrix} \sigma_1 \\ \sigma_2 \\ \sigma_3 \\ \tau_{23} \\ \tau_{13} \\ \tau_{12} \end{bmatrix} \tag{5} \end{equation}The short notation is:
\begin{equation} \boldsymbol{\varepsilon}=\mathbf{S}\boldsymbol{\sigma} \tag{6} \end{equation}Observe that, due to symmetry of the compliance matrix $\mathbf{S}$ (i.e.,$S_{ji}=S_{ij}$), there are only 21 independent elastic constants.
The inverse relation is written
\begin{equation} \begin{bmatrix} \sigma_1 \\ \sigma_2 \\ \sigma_3 \\ \tau_{23} \\ \tau_{13} \\ \tau_{12} \end{bmatrix}= \begin{bmatrix} C_{11} & C_{12} & C_{13} & C_{14} & C_{15} & C_{16} \\ C_{12} & C_{22} & C_{23} & C_{24} & C_{25} & C_{26} \\ C_{13} & C_{23} & C_{33} & C_{34} & C_{35} & C_{36} \\ C_{14} & C_{24} & C_{34} & C_{44} & C_{45} & C_{46} \\ C_{15} & C_{25} & C_{35} & C_{45} & C_{55} & C_{56} \\ C_{16} & C_{26} & C_{36} & C_{45} & C_{56} & C_{66} \end{bmatrix} \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \gamma_{23} \\ \gamma_{13} \\ \gamma_{12} \end{bmatrix} \tag{7} \end{equation}with the short notation \begin{equation}\boldsymbol{\sigma} =\mathbf{C}\boldsymbol{\varepsilon} \tag{8} \end{equation}
The sequence of stresses and strains used in the course is by the incices 1, 2, 3, 23, 13, 12. This is one of two common notations, the other one being the sequence 1, 2, 3, 12, 13, 23.
Orthotropic materials¶
Orthotropic materials have 3 mutually perpendicular symmetry planes.
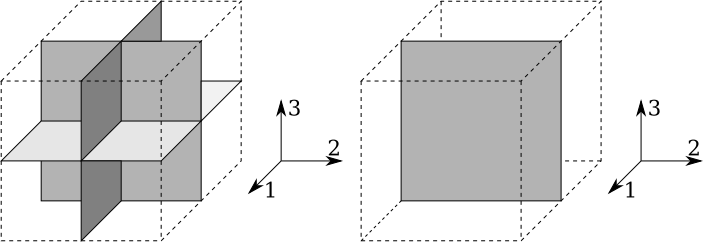
Figure-1: Orthotropic and transversely isotropic symmetry
Due to this symmetry, there are no coupling between normal stresses and shear strains, between shear stresses and normal strains, or between a shear stresses and a shear strains on different planes. Hence, the relation takes the form:
\begin{equation} \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \gamma_{23} \\ \gamma_{13} \\ \gamma_{12} \end{bmatrix} = \begin{bmatrix} S_{11} & S_{12} & S_{13} & 0 & 0 & 0 \\ S_{12} & S_{22} & S_{23} & 0 & 0 & 0 \\ S_{13} & S_{23} & S_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & S_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & S_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & S_{66} \end{bmatrix} \begin{bmatrix} \sigma_1 \\ \sigma_2 \\ \sigma_3 \\ \tau_{23} \\ \tau_{13} \\ \tau_{12} \end{bmatrix} \tag{9} \end{equation}Orthotropic materials have 9 independent elastic constants where the components of the compliance matrix expressed by the engineering constants are:
\begin{equation} \begin{aligned} &S_{11}=\frac{1}{E_1} && S_{22}=\frac{1}{E_2} && S_{33}=\frac{1}{E_3} \\ &S_{12}=-\frac{\nu_{12}}{E_1} && S_{13}=-\frac{\nu_{13}}{E_1} && S_{23}=-\frac{\nu_{23}}{E_2} \\ &S_{44}=\frac{1}{G_{23}} && S_{55}=\frac{1}{G_{13}} && S_{66}=\frac{1}{G_{12}} \end{aligned} \tag{10} \end{equation}where $E_i$ are elastic moduli, $\nu_{ij}$ are Poisson's ratios, and $G_{ij}$ are shear moduli.
From the symmetry of the compliance matric:
\begin{equation} \frac{\nu_{ij}}{E_i} = \frac{\nu_{ji}}{E_j} \tag{11} \end{equation}Example¶
A fictive orthotropic material has the following engineering constants:
import matlib
m1=matlib.newMaterial(E1=150000, E2=20000, E3=10000, v12=0.3, v13=0.4, v23=0.5, G12=5000, G13=4000, G23=3000)
See Material properties and Material Library for explanation of the function newMaterial().
The compliance matrix can conveniently be computed by a function taking the material as an argument:
import numpy as np
def S3D(m):
return np.array(
[[ 1/m['E1'],-m['v12']/m['E1'],-m['v13']/m['E1'], 0, 0, 0],
[-m['v12']/m['E1'], 1/m['E2'],-m['v23']/m['E2'], 0, 0, 0],
[-m['v13']/m['E1'],-m['v23']/m['E2'], 1/m['E3'], 0, 0, 0],
[ 0, 0, 0,1/m['G23'], 0, 0],
[ 0, 0, 0, 0,1/m['G13'], 0],
[ 0, 0, 0, 0, 0,1/m['G12']] ],
float)
Obtaining the compliance matrix and print formatted output by numpy.array2string():
S=S3D(m1)
print(np.array2string(S, precision=6, suppress_small=True, separator=' ', floatmode='maxprec') )
The stiffness matrix $\mathbf{C}$ is now the inverse of the compliance matrix $\mathbf{S}$:
\begin{equation} \mathbf{C}=\mathbf{S}^{-1} \tag{12} \end{equation}Another function taking the material as the only argument:
def C3D(m):
S=S3D(m)
return np.linalg.inv(S)
C=C3D(m1)
print(np.array2string(C, precision=0, suppress_small=True, separator=' ', floatmode='maxprec_equal') )
As previously stated; normal strains cause only normal stress. For example:
strains=[0.003, 0.002, 0.001, 0.0, 0.0, 0.0]
stresses = np.dot(C,strains)
print(np.array2string(stresses, precision=1, suppress_small=True, separator=' ', floatmode='maxprec_equal') )
def solveHookes(C,**kwargs):
# C: the stiffness matrix
# kwargs: prescribed stresses or strains
stress=np.zeros((6))
strain=np.zeros((6))
stressKeys=('s1','s2','s3','s23','s13','s12') # valid stress keys
strainKeys=('e1','e2','e3','e23','e13','e12') # valid strain keys
knownKeys= ['s1','s2','s3','s23','s13','s12'] #initially assume known stresses
knownVals=np.array([0,0,0,0,0,0],float)
for key in kwargs:
if key in stressKeys:
i=stressKeys.index(key)
knownKeys[i]=key
knownVals[i]=kwargs[key]
if key in strainKeys:
i=strainKeys.index(key)
knownKeys[i]=key
knownVals[i]=kwargs[key]
M1=-np.copy(C)
M2= np.copy(C)
ID= np.identity(6)
for k in range(0,6):
if knownKeys[k] in stressKeys:
M2[:,k]=-ID[:,k]
else:
M1[:,k]=ID[:,k]
sol=np.dot( np.linalg.inv(M1), np.dot(M2,knownVals))
for i in range(0,6):
if knownKeys[i] == stressKeys[i]:
stress[i]=knownVals[i]
strain[i]=sol[i]
if knownKeys[i] == strainKeys[i]:
strain[i]=knownVals[i]
stress[i]=sol[i]
return stress,strain
Example, comparing the previous example having $\sigma_1, \varepsilon_2$ and $\sigma_3$ as known nonzero values while assuming that other stresses are zero:
stress, strain = solveHookes(C=C, s1=491.8, e2=0.002, s3=43.46 )
print('stress=', np.array2string(stress, precision=1, suppress_small=True, separator=' ', floatmode='maxprec_equal') )
print('strain=', np.array2string(strain, precision=4, suppress_small=True, separator=' ', floatmode='maxprec_equal') )
Transversely isotropic materials¶
A transversely isotropic material is one with properties that are symmetric about an axis that is normal to a plane of isotropy. This transverse plane has infinite planes of symmetry and thus, within this plane, the material properties are the same in all directions.
Assuming that the plane $2$-$3$ is a plane of isotropy as illustrated in Figure-1, the elastic constants are related by:
\begin{equation} E_3=E_2, \quad \nu_{13}=\nu_{12}, \quad G_{13} = G_{12}, \quad G_{23}=\frac{E_2}{2(1+\nu_{23})} \tag{13} \end{equation}A transversely isotropic material has therefore 5 independent elastic constants.
Unidirectional fiber composites are usually considered to be transversely isotropic.
The proof of the relations (13) is left as an exercise
Isotropic materials¶
Isotropic materials have only 2 independent elastic constants:
\begin{equation} E_{ij}=E, \quad \nu_{ij}=\nu, \quad G_{ij}=G = \frac{E}{2(1+\nu)} \tag{14} \end{equation}Constraints on the engineering constants¶
Both the stiffness matrix and the compliance matrix must be positive definite.
For orthotropic, transversely isotropic and isotropic materials, this requirement implies that every subdeterminat of the main diagonal is positive. For the compliance matrix that is:
\begin{equation} \text{det} \begin{bmatrix} S_{11} & S_{12} & S_{13} & 0 & 0 & 0 \\ S_{12} & S_{22} & S_{23} & 0 & 0 & 0 \\ S_{13} & S_{23} & S_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & S_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & S_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & S_{66} \end{bmatrix} >0 \tag{15} \end{equation}\begin{equation} \text{det} \begin{bmatrix} S_{11} & S_{12} & S_{13} \\ S_{12} & S_{22} & S_{23} \\ S_{13} & S_{23} & S_{33} \end{bmatrix} >0 \tag{16} \end{equation}\begin{equation} \text{det} \begin{bmatrix} S_{11} & S_{12} \\ S_{12} & S_{22} \end{bmatrix} >0, \quad \text{det} \begin{bmatrix} S_{11} & S_{13} \\ S_{13} & S_{33} \end{bmatrix} >0, \quad \text{det} \begin{bmatrix} S_{22} & S_{23} \\ S_{23} & S_{33} \end{bmatrix} >0 \tag{17} \end{equation}\begin{equation} S_{11}>0,\quad S_{22}>0,\quad S_{33}>0,\quad S_{44}>0,\quad S_{55}>0,\quad S_{66}>0 \tag{18} \end{equation}Example
S=S3D(m1)
print('Equation 15: det =', np.linalg.det(S) )
print('Equation 16: det =', np.linalg.det(S[0:3,0:3]) )
Python tips & tricks¶
The functions S3D() and C3D() as well as other common functions can be added to a separate Python file for later use. For example, consider the following content in a file compositelib.py:
import numpy as np
def S3D(m):
'''
Input:
- m: dictionary of material properties
Output:
- returns the compliance matrix as a 6x6 array
'''
return np.array(
[[ 1/m['E1'],-m['v12']/m['E1'],-m['v13']/m['E1'], 0, 0, 0],
[-m['v12']/m['E1'], 1/m['E2'],-m['v23']/m['E2'], 0, 0, 0],
[-m['v13']/m['E1'],-m['v23']/m['E2'], 1/m['E3'], 0, 0, 0],
[ 0, 0, 0,1/m['G23'], 0, 0],
[ 0, 0, 0, 0,1/m['G13'], 0],
[ 0, 0, 0, 0, 0,1/m['G12']] ],
float)
def C3D(m):
'''
Input:
- m: dictionary of material properties
Output:
- returns the stiffness matrix as a 6x6 array
'''
return np.linalg.inv(S3D(m))
If this file exists in the current directory (i.e., where your main Python code is executed) or in any of the search path (dependent on your system), the functions can be accessed by import:
import compositelib
C=compositelib.C3D(m1)
Alternatively:
from compositelib import C3D
C=C3D(m1)
The comments between the two ''' are available by help():
help(compositelib.C3D)


