Sandwich structures¶

The primary idea behind a sandwich structure (there are a few other prominent features as well) is to increase the flexural stiffness without adding much weight to the laminate. This is achieved by using a low-density core material sandwiched between two face sheets.

Foam core materials for structural sandwich composites in light-weight designs comes with densities typically in the range of 50 kg/m³ to 250 kg/m³.

Example: Cross-linked PVC cores with a density of 100 kg/m³ such as Divinycell H100, can be approximated to an isotropic material with a modulus of 100 MPa and Poisson’s ratio of 0.3.

mcore={'name':'H100','rho':100E-12, 'E1':100, 'E2':100, 
       'v12':0.3, 'G12': 100/(2+2*0.3), 'G13': 100/(2+2*0.3), 'G23': 100/(2+2*0.3) }

Computing the bending stiffness $D_b$ of the following sandwich laminate:

from laminatelib import laminateStiffnessMatrix
import numpy as np

def bendingStiffness(layup,b=1):
    # bending stiffness according to equation (1)
    ADB = laminateStiffnessMatrix(layup)
    return ADB[3,3] - (ADB[3,4]**2)/ADB[4,4]

m1= {"name": "E-glass/Epoxy", "rho": 2000E-12, "E1": 40000, "E2": 10000,
     "v12": 0.3, "G12": 3800, "G13": 3800, "G23": 3400}

sandw  = [{'mat':m1,    'ori':0, 'thi':  0.5},
          {'mat':mcore, 'ori':0, 'thi' :16.0},
          {'mat':m1,    'ori':0, 'thi':  0.5} ]

Db_sw = bendingStiffness(sandw)

Iterate to find the required thickness for a monolithic laminate having the same bending stiffness as the sandwich solution:

ts = np.linspace(1,20,1000)
for t in ts:
    monol  = [{'mat':m1,    'ori':0, 'thi': t}]
    Db_mo = bendingStiffness(monol)
    if Db_mo > Db_sw:
        print(t)
        print(Db_mo / Db_sw)
        break

9.387387387387388
1.000006204537707

Computing the ratio of weight per area for the two different solutions:

w_sandw = m1['rho']*1 + mcore['rho']*16
w_monol = m1['rho']*t

print( w_monol/w_sandw )

5.215215215215216

Simplified mechanics of sandwich beams and panels¶

Flexural stiffness and strength of sandwich beams and panels can be approximated reasonably well by simple set of relations when the following requirements are fulfilled:

The sandwich is assumed to be symmetric
The thickness of the face sheets is much less than the thickness of the core, i.e: $t_f << t_c$
The modulus of the core is much less than the effective modulus of the face sheets, i.e: $E_c << E_f$ and the modulus of the core can then be neglected when computing the bending stiffness
The thickness of the sandwich laminate does not change during deformation

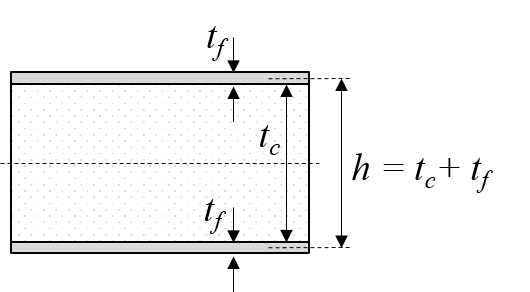
Figure-1: Sandwich, simplified framework

The maximum deflection is a superposition of bending and shear deformation

\begin{equation} w = k_b\frac{FL^3}{D_b} + k_s\frac{FL}{S} \tag{1} \end{equation}

where $k_b$ is a bending deflection coefficient and $k_s$ is a shear deflection coefficient. For a freely supported beam subjected to a center load, their values are 1/48 and 1/4 respectively. For other cases, tabulated coefficient can be found in for example Sandwich design technology manual from Hexcel or in the DIAB Sandwich Handbook.

The bending stiffness is approximated to

\begin{equation} D_b = \frac{E_f t_f b h^2}{2} \tag{2} \end{equation}

while the shear stiffness is

\begin{equation} S = b h G_c \tag{3} \end{equation}

where $E_f$ is the effective modulus ($E_x$) of the face sheet laminates and $G_c$ is the shear modulus ($G_{13}$) of the core.

Note that the difference between equation (2) and

\begin{equation} D_b = b\big ( D_{xx} - \frac{D_{xy}^2}{D_{yy}} \big) \tag{4} \end{equation}

is minor when the assumptions are fulfilled:

tc = 16.0
tf = 0.5
Ef = m1['E1']
Gc = mcore['G13']
b  = 1
h  = tc+tf

sandw  = [{'mat':m1,    'ori':0, 'thi':  tf},
          {'mat':mcore, 'ori':0, 'thi' : tc},
          {'mat':m1,    'ori':0, 'thi':  tf} ]

Db_eq4 = bendingStiffness(sandw,1)

Db_eq3 = (Ef*tf*b*h**2)/2 

print(Db_eq3/Db_eq4)

0.9873192785648663

Example: a freely supported beam subjected to a center load:

kb = 1/48
ks = 1/4
F = 500
L = 250
b = 30
Db = (Ef*tf*b*h**2)/2 
S = b*h*Gc

w_bending = (kb*F*L**3)/Db 
w_shear = ks*F*L/S 
w = w_bending + w_shear

print('Deflection = ', w, 'mm')
print('Contribution from shear deflection is',w_shear,'mm')

Deflection =  3.6341954902560962 mm
Contribution from shear deflection is 1.6414141414141414 mm

The maximum/minimum stress at the bottom face / top face is

\begin{equation} \sigma = \pm \frac{FL}{4 b h t_f} \tag{5} \end{equation}

sigma = (F*L)/(4*b*h*tf)
print('Maximum stress at the mid span is: ',sigma, 'MPa')

Maximum stress at the mid span is:  126.26262626262626 MPa

For a detailed FEA study of a sandwich beam, se the case study FEA of a sandwich beam

Disclaimer:This site is designed for educational purposes only. There are most likely errors, mistakes, typos, and poorly crafted statements that are not detected yet... www.ntnu.edu/employees/nils.p.vedvik