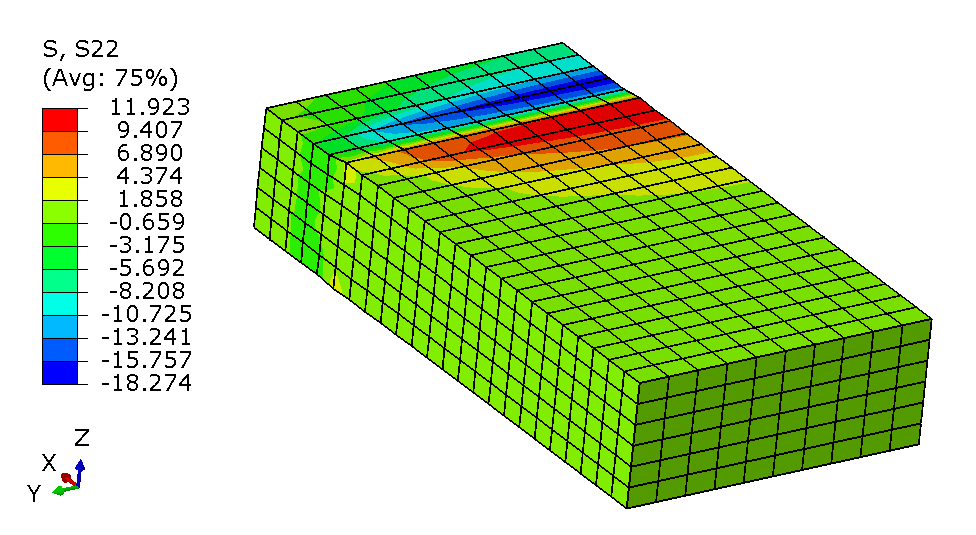
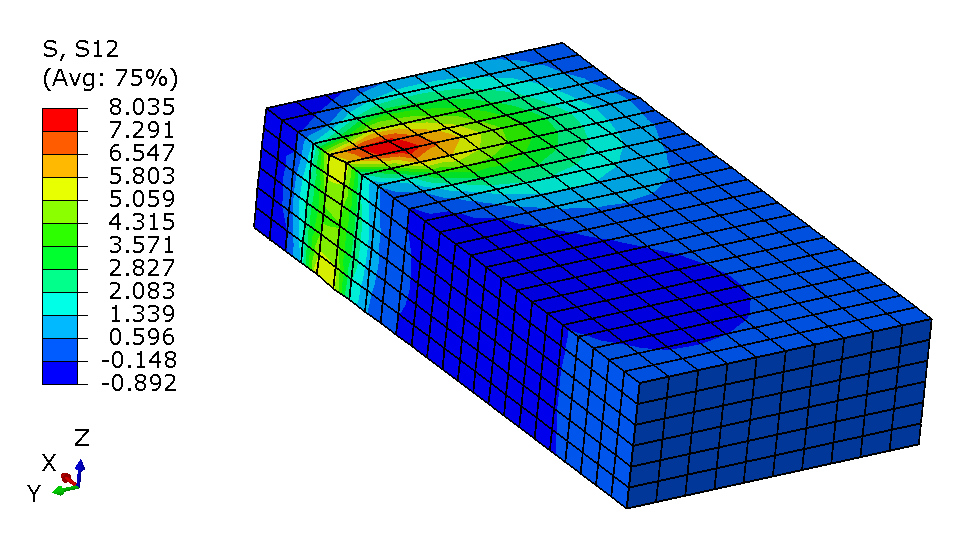
Compression testing of UD composites¶
Properties and dimensions for loading along the 0-direction:¶
- Material: E-glass/Epoxy
- Width $b$ = 10 mm
- Thickness $t$ = 2 mm
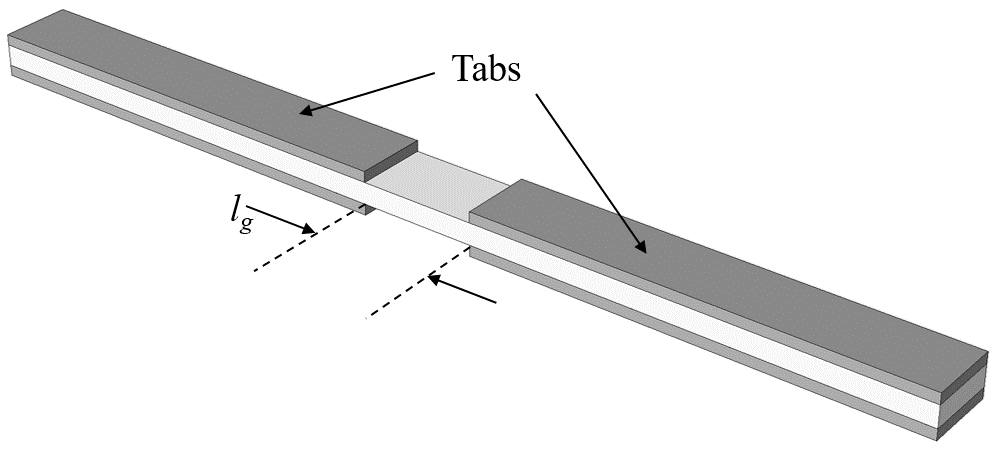
- Tab length = 50 mm
- Gauge length $l_g$: to be decided
According to Euler buckling of a column:
\begin{equation} F_{crit} = - \frac{\pi^2 E I}{(KL)^2} \end{equation}Searching for a gauge length that enables compressive stress well above 1000 MPa (or actually below since it is negative...):
In [1]:
from math import pi
E=40000
b=10
h=2
K=0.5
I = (b*h**3)/12
for L in (25,24,23,22,21,20):
Fc = -((pi**2)*E*I)/((K*L)**2)
print('L=',L,'Fc=',Fc, 's2=',Fc/(2*10))
The results suggest that a gauge length of 20 mm is sufficiently small to avoid premature buckling before compressive failure.
Assumptions for a simplified approach¶
- We can reasonably assume that the first buckling mode is symmetric about both the y-z plane and the x-z plane (x-axis is along the length and y-axis is along the width). Therefore, only a 1/4 of the model is needed.
- The tabs transfer a uniform shear force to the specimen, and the grips imposes a uniform displacement constraint on the specimen. Therefore, we do not need to include the tabs in the model.
Material, orientation and mesh¶
Material properties from E-glass/Epoxy:
In [2]:
import matlib
m=matlib.get('E-glass/Epoxy')
print(m)
- Element size: 0.5 mm
- No. of elements through the thickness: 6
- Element type: C3D8R
Static step and boundary conditions¶
According to the assumptions:
- Symmetrical BC about the y-z plane
- Symmetrical BC about the x-z plane
- Fixed uz on surfaces connecting to the tabs
Loading¶
- Compressive normal stress: -1000 MPa
- Need to compute the corresponding shear stress (traction) on the tab's area:
In [3]:
s2 = -1000 # compressive stress (MPa)
force = s2*5*2 # stress multiplied with cross section area
shear = force/(5*50*2) # shear traction (MPa) on tab's surface (both sides)
print('shear traction to be imposed:',shear)
In [4]:
eigenvalue = 0.73287
s1_applied = -1000
s1_atBuckling = eigenvalue*s1_applied
print(s1_atBuckling)
Apparantly, the Euler buckling theory is not applicable for this case when the FEA result is jugded more accurate. Hence, the thickness should be increased or the gauge length should be reduced. See the recomendation given in Test methods based on ASTM 3410.
Further interpretation of results is left as exercise.